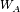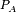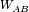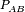Probabilities module¶

The probabilities module contains a classes that allow the calculation of weigth and probability matrixes for mixed-layer minerals.

Theory¶

Mixed-layer probabilities¶

These probability classes use the Reichweite (= R) concept and Markovian statistics to calculate how the layer stacking sequence is ordered (or disordered).

The value for R denotes what number of previous layers (in a stack of layers) still influence the type of the following component. With other words, for:

R=0; the type of the next component does not depend on the previous components,

R=1; the type of the next component depends on the type of the previous component,

R=2; the type of the next component depends on the type of the previous 2 components,

…

We can describe the stacking sequence using two types of statistics: weight fractions and probabilities. Some examples:

the fraction of A type layers would be called $W_A$

the probability of finding an A type layer in a stack would be called $P_A$

the fraction of A type layers immediately followed by a B type layer would be called $W_{AB}$

the probability of finding an A type layer immediately followed by a B type layer would be called $P_{AB}$

There exist a number of general relations between the weight fractions W and probabilities P which are detailed below. They are valid regardless of the value for R or the number of components G. Some of them are detailed below. For a more complete explanation: see Drits & Tchoubar (1990). For stacks composed of G types of layers, we can write (with 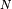$N$ the number of layers):

$\begin{align*} & \begin{aligned} & W_{i} = \frac{N_{i}}{N_{max}} &\forall i \in \left[{1,2,\dots,G}\right] \\ & W_{ij} = \frac{N_{ij}}{N_{max}-1} &\forall i, j \in \left[{1,2,\dots,G}\right] \\ & W_{ijk} = \frac{N_{ijk}}{N_{max}-2} &\forall i, j, k \in \left[{1,2,\dots,G}\right] \\ & \text{etc.} \\ \end{aligned} \quad \quad \begin{aligned} & W_{ij} = W_i \cdot P_{ij} \\ & W_{ijk} = W_{ij} \cdot P_{ijk} \\ & \text{etc.} \\ \end{aligned} \quad \quad \begin{aligned} & \sum_{i=1}^{G}{W_i} = 1 \\ & \sum_{i=1}^{G}{\sum_{j=1}^{G}{W_{ij}}} = 1 \\ & \text{etc.} \\ \end{aligned} \quad \quad \begin{aligned} & \sum_{j=1}^{G}{P_{ij}} = 1 \\ & \sum_{k=1}^{G}{P_{ijk}} = 1 \\ & \text{etc.} \\ \end{aligned} \\ \end{align*}$

Because of these relationships it is not neccesary to always give all of the possible weight fractions and probability combinations. Each class contains a description of the number of ‘independent’ variables required for a certain combination of R ang G. It also details which ones were chosen and how the others are calculated from them.

More often than not, ratios of several weight fractions are used, as they make the calculations somehwat easier. On the other hand, the actual meaning of these fractions is a little harder to grasp at first.

Class functionality¶

The classes all inherit from an ‘abstract’ base class which provides a number of common functions. One of the ‘handy’ features are its indexable properties mW and mP. These allow you to quickly get or set an element in one of the matrixes:

>>> from pyxrd.probabilities.models import R1G3Model
>>> prob = R1G3Model()
>>> prob.mW[0] = 0.75 # set W1
>>> print prob.mW[0]
0.75
>>> prob.mW[0,1] = 0.5 # set W12
>>> print prob.mW[0,1]
0.5

Note however, that doing so might produce invalid matrices and produce strange X-ray diffraction patterns (or none at all). It is therefore recommended to use the attributes of the selected ‘independent’ parameters (see previous section) as setting these will trigger a complete re-calculation of the matrices.

If however, you do want to create a matrix manually, you can do so by setting all the highest-level elements, which are:

for an R0 class only the Wi values

for an R1 class the Wi and Pij values

for an R2 class the Wij and Pijk values

for an R3 class the Wijk and Pijkl values

After this you can call the solve and validate methods, which will calculate the other values (e.g. for an R2 it will calculate Wi, Wijk and Pij values).

An example:

>>> from pyxrd.probabilities.models import R1G2Model
>>> prob = R1G2Model()
>>> prob.mW[0] = 0.75 # set W1
>>> prob.mW[1] = 0.25 # set W2 (needs to be 1 - W1 !)
>>> prob.mP[1,1] = 0.3 # set P22
>>> prob.mP[1,0] = 0.7 # set P21 (needs to be 1 - P22 !)
>>> prob.mP[0,1] = 0.7 / 3.0 # set P12 (needs to be P21 * W2 / W1!)
>>> prob.mP[0,0] = 2.3 / 3.0 # set P11 (needs to be 1 - P12 !)
>>> prob.solve()
>>> prob.validate()
>>> print prob.get_distribution_matrix()
[[ 0.75  0.  ]
 [ 0.    0.25]]
>>> print prob.get_probability_matrix()
[[ 0.76666667  0.23333333]
 [ 0.7         0.3       ]]

Note that at the end we print the validation matrixes to be sure that we did a good job: if all is valid, we should see only “True” values. For more details on what elements produced an invalid results, you can look at the W_valid_mask and P_valid_mask properties.

The exact same result could have been achieved using the independent parameter properties:

>>> from pyxrd.probabilities.models import R1G2Model
>>> prob = R1G2Model()
>>> prob.W1 = 0.75
>>> prob.P11_or_P22 = 0.3
>>> print prob.get_distribution_matrix()
[[ 0.75  0.  ]
 [ 0.    0.25]]
>>> print prob.get_probability_matrix()
[[ 0.76666667  0.23333333]
 [ 0.7         0.3       ]]

For more information see the _AbstractProbability class

Models¶

Base Models¶

R0 Models¶

R0 models have 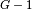$G - 1$ independent parameters, 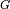$G$ being the number of components.

Partial weight fractions were chosen as independent parameters, as this approach scales very well to a large number of components:

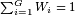If we define a partial weight fraction as $F_i = \frac{W_i}{\sum_{j=i}^{G}{W_j}} \forall i \in \left[ {1,G} \right]$ , and keep in mind the general rule $\sum_{i=1}^{G}{W_i} = 1$ , we can calculate all the weight fractions from these partial weight fractions progressively, since:

$F_1$ will acutally be equal to $W_1$ .

the denominator of every fraction $F_i$ is equal to $1 - \sum_{j=1}^{i-1}{W_j}$ , and you are able to calculate this:

for $F_2$ , it would be $1 - W_1$ , and you know $W_1$ from the first fracion

for $F_3$ it would be $1 - W_1 - W_2$ , and you can get $W_1$ and $W_2$ from the previous two fractions.

once the weight fractions of the first $G - 1$ components are known, then the weight fractions of the last component can be calculated as $W_g = 1 - \sum_{i=1}^{G}{W_i}$ .

Probabilities module¶

Theory¶

Mixed-layer probabilities¶

Class functionality¶

Models¶

Base Models¶

R0 Models¶

R1 Models¶

R2 Models¶

R3 Models¶

Table Of Contents

Previous topic

Next topic

This Page